CultureMath
Ressources adaptées au programme de mathématiques de terminale S
Le programme des premières S (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes (plus deux pour l'enseignement de spécialité), et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Analyse
- Géométrie
- Statistique et probabilités
- Arithmétique (enseignement de spécialité)
- Matrices et suites (enseignement de spécialité)
Deux capacités transversales :
Un livre de plus en probabilités statistique? Comprendre pour faire, puis faire pour comprendre : cet ouvrage, remis à jour en 2008, est destiné à tous les enseignants de l’enseignement secondaire et supérieur et aux étudiants de premier cycle universitaire.Comprendre pour faire : l’originalité de ce livre réside dans la première partie, où l’auteur prend le temps de développer les aspects historiques et culturels des probabilités : hasard et modèles, risques, principe de précaution, espérance et jeux, médecine, biologie, mathématiques financières…
L’idée fondamentale est d’aborder les Mathématiques de Première et Terminale S par le biais d’un élément familier et le plus souvent apprécié des jeunes. La question de l’utilité des Mathématiques formelles (dépassant le simple calcul) dans leur vie quotidienne donne souvent lieu à des débats avec les élèves. Montrer les héros de séries TV (objet d’identification par le spectateur) aux prises avec des problèmes mathématiques pratiques peut leur permettre de mieux appréhender cette utilité...
C'est l'héroine de l'histoire, mathématicienne, écrivain, femme engagée, libre, en un mot : vivante. Commençons par la toupie, jeu d'enfant bien (?) connu mais également objet qui fascine depuis longtemps les mathématiciens. Une toupie un peu idéalisée, bien entendu, dont les évolutions prennent le nom de "mouvement d'un solide pesant autour d'un point fixe"...
Les Coniques d’Apollonius de Perge constituent l’un des sommets de la géométrie grecque ancienne. Rédigé, après un premier essai, en huit Livres, leur destinée fut cependant moins heureuse que celle des Éléments d’Euclide. Seuls les quatre premiers Livres — selon l’auteur ils exposent les “éléments” de la théorie — ont été conservés en grec, dans la réédition qu’en procura, à la charnière des Ve et VIe siècles de notre ère, Eutocius d’Ascalon. Les Livres V-VII furent préservés grâce à la traduction arabe qu’en fit Thâbit ibn Qurra mais ils restèrent inaccessibles et excitèrent l’imagination des mathématiciens d’Occident pendant plusieurs siècles.
Dès l’Antiquité, la rigueur et la généralité du traitement apollinien avait été reconnues et avait fait disparaître les écrits antérieurs. Seules quelques bribes d’information, quelques conjectures hasardeuses concernant la découverte des coniques nous ont été transmises par Pappus et Eutocius.
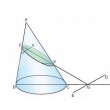
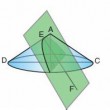
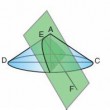
On coupe un cône quelconque de sommet A ayant le cercle de diamètre BC comme base par deux plans, l'un passant par l'axe du cône, comme ABC, l'autre coupant la génératrice AB en F et la base du cône selon une droite DE, de telle manière qu'elle soit perpendiculaire au diamètre BC ou à son prolongement...
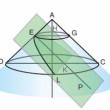
On mène par E, situé sur la génératrice AD, un plan perpendiculaire à AD. La droite EP est l'intersection de ce plan avec le plan méridien du cône DAC. Soit K un point quelconque de EP...
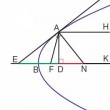
Soit une parabole de sommet B et d'axe BK. On mène en A la tangente EAG qui coupe l'axe en E. On mène AN et AD perpendiculaires respectivement à EG et BK. AN s'appelle la normale en A, ED la sous-tangente et DN la sous-normale...
Le Livre VII de la Collection mathématique de Pappus d'Alexandrie se présente comme un companion destiné à faciliter la lecture d'un corpus de textes, dit « du Lieu analysé », composé de douze traités dus à quatre auteurs...
On a deux droites données A, E. Il faut, entre elles, intercaler deux droites moyennes proportionnelles, disons B, C. Autrement dit on doit avoir A : B :: B : C :: C : E...
Nous proposons de présenter la précision et la généralisation faites par Du Bois-Reymond et par Lebesgue de la condition d’intégrabilité R2.