CultureMath
[1] Approximation diophantienne et réseaux
[2] Une démonstration originale de l'infinité de l'ensemble des nombres premiers
[3] Sur l'algorithme RSA
[4] Arithmétique
[5] Fermat revisité
[6] Le problème des nombres gelés de Saint-Exupéry
[7] Les mathématiques du mouvement Introduction informelle aux systèmes dynamiques
[8] Petits pièges de la simulation numérique
[9] Le théorème de Sharkovskii
[10] Arbres et dérivée d'une fonction composée
[11] Homographies et suites récurrentes
[12] L'intégration selon Riemann et selon Lebesgue
[13] Signal numérique et théorie de l'échantillonnage
[14] Les intégrales de Coxeter
[15] Equirépartition d'une suite de nombres
[16] Addendum sur l'équirépartition
[17] Racine carrée fonctionnelle
[18] Le lemme de Baire
[19] Le théorème de JUEL et la surface de CLEBSCH
[20] Critères d'Ermakov
[21] Le produit d'Hadamard de deux séries entières
[22] Racine carrée fonctionnelle
[23] Jauge d'une cuve à Mazout
[24] Sur les nombres constructibles
[23] Construction des polygones réguliers
[26] Courbure des surfaces triangulées
[27] Le problème des 5 cercles
[28] Reconnaître effectivement les Ensembles Algébriques Réels
[29] Pour nouer, il faut courber
[30] Autour des triangles inscrits sur une hyperbole équilatère
[31] Gaspard Monge, de la planche `a dessin aux lignes de courbure
[32] Loi de groupe dans un triangle
[33] Les épi ou hypo trochoïdes
[34] Géométrie sur une Strophoïde
[35] Fermeture Hexagonale
[36] Cubiques circulaires passant par leurs foyers singuliers
[37] Combien de fois faut-il battre un jeu de cartes ?
[38] Avant le référendum
[39] La percolation
[40] Processus de branchement et descendance d'un individu
[41] Marches aléatoires sur Z
[42] Le jeu de Pile ou Face
[43] Le Berlekamp's switching game
[44] Jeux sur les graphes et théorème de Ramsey
[45] Jeux et stratégies
[46] Equations algébriques
[47] Intégration de polynômes, points de Gauss
[48] Les tonalités musicales vues par un mathématicien
[49] Loi de groupe sur une surface
[50] La transformation du Boulanger
[51] Rubik’s cube, groupe de poche
[52] Compte de rebonds
[53] La toupie Tippe-Top
[54] Détermination du sexe selon la température chez les crocodiles
[55] Calcul Tensoriel. Application à la relativité.
[56] Equations de Maxwell et formes différentielles, vers la relativité restreinte
[57] Les motifs des pelages d’animaux
[58] Les cercles de Tücker
[59] Interactions entre espèces, modèle de Lotka-Volterra
[60] Équation de la chaleur : traitement numérique
[61] Simulation numérique de l'équation de la chaleur
[62] Du bruit dans les images
[63] Image and movie denoising by nonlocal means
[64] Construction des entiers naturels
[65] Les axiomes de Zermelo-Fraenkel
[66] Entiers relatifs
[67] Nombres rationnels
[68] Nombres réels
[69] Nombres complexes
[70] Quaternions
[71] Ordinaux
[72] La construction des Réels par les coupures de Dedekind
[73] Laplace, Turing et la géométrie impossible du "jeu de l'imitation"
[74] La divination sikidy à Madagascar
[75] Les généralisations de la notion mathématique d'intégrale au 19e siècle
[76] Le processus d'abstraction dans le développement des premières théories de la mesure
[77] Les deux premiers journaux mathématiques français: les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1845)
[78] Pourquoi, pour qui enseigner les mathématiques? Une mise en perspective historique des finalités et des contenus de l'enseignement des mathématiques dans la société française au XXe siècle.
[79] Les matrices : formes de représentation et pratiques opératoires (1850-1930)
[80] La loi des grands nombres, le théorème de De Moivre-Laplace
[81] La formule de Stirling
[82] Urnes aléatoires, populations en équilibre et séries génératrices
[83] Zeta de 3 est irrationnel
[84] Généalogie de populations : le coalescent de Kingman
[85] Cantor et la France
[86] Introduction à la Théorie des Groupes
[87] À la recherche de la genèse du dernier mémoire mathématique de Georg Cantor
[88] Le triangle: philosophie, histoire, mathématiques
[89] Au menu: de la géométrie à toutes les sauces
[90] Gaston DARBOUX : « Principes de Géométrie Analytique »
[91] "Souvenirs sur Sofia Kovalevskaya" de Michèle Audin
[92] Eléments d'analyse et d'algèbre (et de théorie des nombres)
[93] Pourquoi les mathématiques sont-elles difficiles ?
[94] Souvenirs sur Sofia Kovalevskaya - interview/discussion avec Michèle Audin
[96] Analyse mathématique - La maîtrise de l'implicite
[97] Epistémologie mathématique
[98] Galois, le mathématicien maudit
[99] Les Clefs pour la PSI et la PSI*
[100] Blagues mathématiques et autres curiosités
[101] Escapades arithmétiques
[102] Le jardin des courbes - Dictionnaire raisonné des courbes planes célèbres et remarquables
[101] Le problème de l'espace. Sophus Lie, Friedrich Engel et le problème de Riemann-Helmholtz
[102] Riemann : Le géomètre de la nature
[103] Eléments d'analyse et d'algèbre (et de théorie des nombres) (présentation par l’auteur)
[104] La construction tractionnelle des équations différentielles
[105] Géométrie analytique classique
[106] La passeggiata - Battements d'ailes au jardin du Luxembourg
[107] Vers une nouvelle philosophie de la nature
[108] Probabilités et statistiques aujourd'hui
[109] Des Mathématiciens de A à Z
[110] Souvenirs sur Sofia Kovalevskaya (parutions)
[111] Cantor et la France
[112] Dimensions
[113] Arithmétique
[114] La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs
[115] Premiers cours de philosophie positive
[116] Une Introduction à la théorie des nombres
[117] Outils mathématiques à l’usage des scientifiques et ingénieurs
[118] Nombres : Eléments de mathématiques pour philosophes
[119] Images des Mathématiques 2004-2006
[120] Leçons de mathématiques d'aujourd'hui
[121] Zoom sur les métiers des mathématiques
[122] Autour du centenaire Lebesgue
[123] L'épistémologie : état des lieux et positions
[124] Philosophie naturelle et géométrie au XVIIe siècle
[125] Les Mathématiques dans la Cité
[126] Réduction des endomorphismes
[127] Les femmes et l'enseignement scientifique
[128] Exercices de mathématiques pour physiciens
[129] La Relativité de Poincaré de 1905
[130] L'espace physique entre mathématiques et philosophie
[131] Jacques Hadamard, un mathématicien universel
[131] Un mathématicien d'exception
[132] Nouvelle bibliographie cournotienne
[133] Paul Painlevé (1863-1933). Un savant en politique
[134] La naissance de la théorie de l'information ou la force d'une idée simple
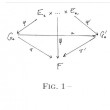
Cet article audacieux entreprend la recherche des 27 droites sur une surface cubique non réglée, avec représentation paramétrique, double six de Schlaffli, lien avec la théorie des groupes et même lien avec la théorie des super-cordes.
Il s'agit d'étalonner une jauge de cuve à Mazout cylindrique bombée, horizontale, et d'utiliser du calcul intégral pour établir la formule exacte de cette jauge.
Les mathématiques ne sont pas l'affaire des seuls mathématiciens: c'est ce que montre le physicien Hubert Krivine dans ce livre. Les mathématiciens ne peuvent que s'en féliciter: c'est le sens de cette préface. Quelques commentaires sont peut-être utiles...
Nous montrons que Poincaré, dans son article de 1905, adopte un point de vue actif concernant le groupe des Transformations de Lorentz...
Ce texte a pour objectif de présenter, de la façon la plus simple possible, les fondements mathématiques de la théorie de la Relativité (surtout générale) ; ces fondements constituent les bases de la branche des mathématiques appelée Calcul Tensoriel. A l'inverse des présentations habituelles qui, centrées sur la Relativité, donnent une liste rapide de quelques définitions et résultats pratiques indispensables de calcul tensoriel, cette étude s'intéresse avant tout aux bases mathématiques de la théorie physique qu'est la Relativité.
L'espace de la relativité générale n'est pas celui de la physique quantique. L'espace de Newton n'est pas celui de Riemann, ou d'Alain Connes. Physiciens, philosophes, et mathématiciens n'ont cessé de discuter et de modifier la notion d'espace, d'en critiquer le statut et la pertinence : réalité ou illusion, objet physique ou entité métaphysique...?
Ce livre raconte l'histoire d'un grand mathématicien dont la vie et l'oeuvre ont embrassé d'importants secteurs, tant scientifiques que politiques. Jacques Hadamard, tout au long d'une carrière qui s'est déroulée à la charnière des XIX e et XX e siècles, s'est intéressé à de nombreux domaines du champ des mathématiques : théorie des nombres, analyse mathématique, mécanique...
La formule dite de Stirling, qui donne une évaluation de n! pour les grandes valeurs de n, est au centre des travaux menés au début du XVIIIe siècle sur les problèmes probabilistes de passage à la limite et d'approximations. Cet article peut se présenter comme un complément au texte sur le théorème de de Moivre-Laplace. La découverte des évaluations de n! par de Moivre et Stirling a donné lieu à des travaux concomitants de ces deux mathématiciens avec des échanges de correspondance, des corrections mutuelles d'erreurs. Ces travaux se situent à un moment que l'on peut qualifier de paradoxal dans l'histoire des mathématiques. En effet les méthodes infinitésimales se développent alors de plus en plus ; elles permettent d'aborder et de résoudre des questions nouvelles. Mais la véracité des résultats obtenus ne peut plus être légitimée par une synthèse démonstrative à la grecque. Il faut donc innover, expérimenter, confronter les résultats obtenus par différentes méthodes ou différents auteurs, avant de pouvoir être sûr de la scientificité d'un énoncé. Nous savons de plus aujourd'hui que certains outils étaient employés sans la rigueur (au sens moderne du terme) nécessaire. Ce sont donc les tours et détours des démarches analytiques du début du XVIIIe siècle que nous voudrions montrer dans ce texte.
Le couple fréquence-probabilité, ainsi que la théorie instituant ce rapport qu'on peut appeler schématiquement "loi des grands nombres", est un leitmotiv de la période classique de l'histoire du calcul des probabilités. Il est au coeur du développement de la théorie et des préoccupations des probabilistes, comme de ses utilisateurs. Les programmes des lycées imposent de prendre une approche fréquentiste pour définir une probabilité. Cela pose le problème du statut de ces énoncés que l'on rassemble sous le nom de "loi des grands nombres". Peu de propositions mathématiques portent ce titre de "loi". Est-ce un théorème, comme il est utilisé habituellement pour le théorème de De Moivre-Laplace ? Est-ce un énoncé extra-mathématique, admis comme prémisse à toute théorie scientifique ?
Les bibliographies consacrées à l’œuvre majeure d’Augustin Cournot sont presque toujours fragmentaires, tant les domaines qu’il a explorés sont divers : mathématiques, économie, philosophie, histoire, sociologie, pédagogie. Or la pensée de Cournot est suffisamment riche et profonde pour ménager un réseau de passages d’un champ à l’autre.