CultureMath
Ressources adaptées au programme de mathématiques de seconde
Le programme du cycle 4 (5e, 4e, 3e ; rentrée 2016) est disponible en version pdf.
Il est découpé en quatre grands thèmes, et assorti de l'enseignement de l'informatique et des EPI. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Nombres et calculs ;
- Organisation et gestion de données, fonctions ;
- Grandeurs et mesures ;
- Espace et géométrie
- Enseignement de l'informatique
- EPI (Enseignements pratiques interdisciplinaires)
Depuis plus de dix ans, La main à la pâte contribue activement à une rénovation de l’enseignement des sciences en France et dans une trentaine de pays. Dans cet esprit, Le Pommier a, en 2004, publié L’Europe des découvertes, destiné aux enseignants de cycle 3 et début collège. L'originalité de l'ouvrage était de permettre une utilisation constructive de l’histoire des sciences et des techniques pour conduire des activités expérimentales en classe....
Après la floraison des IIIe-IIe siècles, les institutions savantes alexandrines, confrontées aux incertitudes politiques et aux querelles dynastiques, connaissent une éclipse. Les recherches mathématiques se poursuivent sans doute ailleurs, notamment à Rhodes, mais, semble-t-il grâce à l’intervention puis la protection des Romains, l’ancienne capitale des Ptolémées va connaître un nouvel âge d’or mathématique. Trois grandes figures dominent les deux premiers siècles de notre ère : Ménéalos, Ptolémée et Héron. Leurs travaux reprennent, corrigent et développent ceux de leurs prédécesseurs de la première période alexandrine, notamment dans les domaines où la géométrie trouve ses applications les plus efficientes : astronomie, optique, mécanique.
Soit AB une corde sous-tendue par l'angle AKB et AC la corde sous-tendue par l'angle supplémentaire. BC est donc un diamètre donc le triangle ABC est rectangle en A et, d'après le théorème de l'hypoténuse (Euclide, I. 47), on a ...
Une aire carrée ayant l'aire plus le périmètre : 896 pieds. Séparer l'aire du périmètre. Je fais ainsi ...
Certains nombres ont acquis un prestige particulier, en raison de leurs propriétés mathématiques, de leurs multiples applications et aussi de la « part de rêve » qu’ils nous donnent au travers de ce qui constitue parfois une véritable mythologie...
Les Coniques d’Apollonius de Perge constituent l’un des sommets de la géométrie grecque ancienne. Rédigé, après un premier essai, en huit Livres, leur destinée fut cependant moins heureuse que celle des Éléments d’Euclide. Seuls les quatre premiers Livres — selon l’auteur ils exposent les “éléments” de la théorie — ont été conservés en grec, dans la réédition qu’en procura, à la charnière des Ve et VIe siècles de notre ère, Eutocius d’Ascalon. Les Livres V-VII furent préservés grâce à la traduction arabe qu’en fit Thâbit ibn Qurra mais ils restèrent inaccessibles et excitèrent l’imagination des mathématiciens d’Occident pendant plusieurs siècles.
Dès l’Antiquité, la rigueur et la généralité du traitement apollinien avait été reconnues et avait fait disparaître les écrits antérieurs. Seules quelques bribes d’information, quelques conjectures hasardeuses concernant la découverte des coniques nous ont été transmises par Pappus et Eutocius.
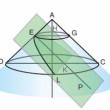
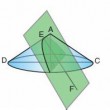
On coupe un cône quelconque de sommet A ayant le cercle de diamètre BC comme base par deux plans, l'un passant par l'axe du cône, comme ABC, l'autre coupant la génératrice AB en F et la base du cône selon une droite DE, de telle manière qu'elle soit perpendiculaire au diamètre BC ou à son prolongement...
On mène par E, situé sur la génératrice AD, un plan perpendiculaire à AD. La droite EP est l'intersection de ce plan avec le plan méridien du cône DAC. Soit K un point quelconque de EP...
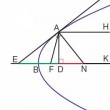
Soit une parabole de sommet B et d'axe BK. On mène en A la tangente EAG qui coupe l'axe en E. On mène AN et AD perpendiculaires respectivement à EG et BK. AN s'appelle la normale en A, ED la sous-tangente et DN la sous-normale...
Le Livre VII de la Collection mathématique de Pappus d'Alexandrie se présente comme un companion destiné à faciliter la lecture d'un corpus de textes, dit « du Lieu analysé », composé de douze traités dus à quatre auteurs...