CultureMath
Ressources adaptées au programme de mathématiques de terminale ES/L
Le programme commun des terminales ES et L (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes, et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
Deux capacités transversales :
Dans la tradition musicale savante occidentale (et cela vaut aussi pour les traditions savantes non occidentales comme la tradition chinoise), la musique a toujours été associée aux mathématiques. Dans le contexte de sociétés sans écriture, en revanche, cette association peut paraître plus surprenante. Le but de cet article est de montrer quelques cas de répertoires musicaux de tradition orale dans lesquels on peut mettre en évidence des structures musicales complexes comparables à des constructions mathématiques.
On peut montrer que sous certaines conditions la structure en escalier est logiquement équivalente à la structure de canon. On représente les formules de harpe comme des mots binifinis sur l'ensemble des couples de cordes noté C, c'est-à-dire des applications de Z dans C. L’ensemble des valeurs de u est la partie C' des couples de C apparaissant dans u.
Après la floraison des IIIe-IIe siècles, les institutions savantes alexandrines, confrontées aux incertitudes politiques et aux querelles dynastiques, connaissent une éclipse. Les recherches mathématiques se poursuivent sans doute ailleurs, notamment à Rhodes, mais, semble-t-il grâce à l’intervention puis la protection des Romains, l’ancienne capitale des Ptolémées va connaître un nouvel âge d’or mathématique. Trois grandes figures dominent les deux premiers siècles de notre ère : Ménéalos, Ptolémée et Héron. Leurs travaux reprennent, corrigent et développent ceux de leurs prédécesseurs de la première période alexandrine, notamment dans les domaines où la géométrie trouve ses applications les plus efficientes : astronomie, optique, mécanique.
Soit AB une corde sous-tendue par l'angle AKB et AC la corde sous-tendue par l'angle supplémentaire. BC est donc un diamètre donc le triangle ABC est rectangle en A et, d'après le théorème de l'hypoténuse (Euclide, I. 47), on a ...
Une aire carrée ayant l'aire plus le périmètre : 896 pieds. Séparer l'aire du périmètre. Je fais ainsi ...
Certains nombres ont acquis un prestige particulier, en raison de leurs propriétés mathématiques, de leurs multiples applications et aussi de la « part de rêve » qu’ils nous donnent au travers de ce qui constitue parfois une véritable mythologie...
Les mathématiques discrètes sont la partie des mathématiques qui s’intéresse à des objets «énumérables » comme une succession de nombres entiers, un réseau routier fait de carrefours reliés par des routes, le codage et l’interprétation de données mises sous la forme d’une suite de 0 et de 1, etc. Encore balbutiantes au début du XXe siècle, les mathématiques discrètes ont, depuis, pris leur essor, notamment sous l’impulsion de l’informatique...
Un livre de plus en probabilités statistique? Comprendre pour faire, puis faire pour comprendre : cet ouvrage, remis à jour en 2008, est destiné à tous les enseignants de l’enseignement secondaire et supérieur et aux étudiants de premier cycle universitaire.Comprendre pour faire : l’originalité de ce livre réside dans la première partie, où l’auteur prend le temps de développer les aspects historiques et culturels des probabilités : hasard et modèles, risques, principe de précaution, espérance et jeux, médecine, biologie, mathématiques financières…
Cet ouvrage s'adresse à tous ceux qui veulent s’initier à la théorie des graphes. Conçu pour comprendre facilement les bases, il permet de débroussailler un peu le terrain avant d'aborder des notions plus complexes. Les novices, sans culture mathématique particulière, peuvent donc le lire sans crainte de se trouver perdus, en tout cas jusqu’au chapitre 4 à partir duquel quelques connaissances sur les matrices puis, plus loin, sur les probabilités et les suites sont nécessaires...
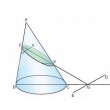
Les Coniques d’Apollonius de Perge constituent l’un des sommets de la géométrie grecque ancienne. Rédigé, après un premier essai, en huit Livres, leur destinée fut cependant moins heureuse que celle des Éléments d’Euclide. Seuls les quatre premiers Livres — selon l’auteur ils exposent les “éléments” de la théorie — ont été conservés en grec, dans la réédition qu’en procura, à la charnière des Ve et VIe siècles de notre ère, Eutocius d’Ascalon. Les Livres V-VII furent préservés grâce à la traduction arabe qu’en fit Thâbit ibn Qurra mais ils restèrent inaccessibles et excitèrent l’imagination des mathématiciens d’Occident pendant plusieurs siècles.
Dès l’Antiquité, la rigueur et la généralité du traitement apollinien avait été reconnues et avait fait disparaître les écrits antérieurs. Seules quelques bribes d’information, quelques conjectures hasardeuses concernant la découverte des coniques nous ont été transmises par Pappus et Eutocius.