CultureMath
Ressources adaptées au programme de mathématiques de première S
Le programme des premières S (B.O. 2010) est disponible en version pdf.
Il est découpé en trois grands thèmes, et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
Deux capacités transversales :
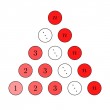
Question du jeudi #39 : On place n points sur un cercle et l'on trace toutes les cordes reliant ces deux points. On suppose en outre que les cordes sont en position générale, c'est-à-dire que trois cordes ne sont jamais concourantes. Combien de points d'intersection y aura-t-il à l'intérieur du disque ?
Question du jeudi #37 : Ana aime le hasard et déteste la monotonie. Tous les matins, elle tire à pile ou face sa boisson pour le petit déjeûner : thé ou café. Elle souhaite ainsi éviter de boire la même chose trois jours de suite. Au bout de n jours, quelle est la probabilité que sa règle de non-monotonie ait été respectée ?
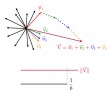
Question du jeudi #36 : On se donne $n$ vecteurs $\vec v_1, \ldots, \vec v_n$ du plan dont la somme des longueurs vaut $1$. Montrer qu'il est possible de trouver une partie $S \subset \{1, 2, \ldots, n\}$ telle que la somme correspondante \[ \sum_{i \in S} \vec v_i\] ait une longueur au moins égale à $\frac 16$.
Titre : Nombres à compter et à raconter
Auteur : Stella Baruk
Éditeur : Le Seuil
Prix : 13,5 €
Un des exercices du Google Code Jam de 2008 demandait de calculer les trois derniers chiffres avant la virgule du nombre $(3+\surd 5)^n$. On explique ici comment calculer ces chiffres presque instantanément en exploitant une jolie propriété arithmétique de $3+\surd 5$.
En partant de la célèbre formule $1 + 2 + \cdots + n = \frac{n(n+1)}2$, on explore les formules donnant la somme des $n$ premières puissances $p$-ièmes.
Le centre Virchow-Villermé propose un MOOC (massive online open course, c'est-à-dire cours en ligne ouvert et massif) intitulé « Fondamentaux en statistique ».
On apprend à tout étudiant débutant que la probabilité d'amener face en deux coups, au jeu de pile ou face, est 3/4 ... et D'Alembert propose ici 2/3. "L'esprit de d'Alembert, habituellement juste et fin, déraisonnait complètement sur le Calcul des probabilités", disait Joseph Bertrand en 1889. Est-ce si sûr ?
Dans le tome IV de ses Opuscules mathématiques, publié en 1768, D'Alembert écrit: "Il y a près de trente ans que j'avois formé ces doutes en lisant l'excellent livre de M. Bernoulli de Arte conjectandi". Les premiers doutes de D'Alembert sur le calcul des probabilités remontent donc environ à 1740, mais pour le moment personne n'en a trouvé trace dans ses manuscrits ni dans ses imprimés de la décennie quarante, dont aucun n'est consacré à de tels sujets.
L'article provient de Chambers, sauf la partie centrale, la plus longue, sur les causes de l'inclinaison des orbites des planètes, qui est de D'Alembert et que nous reproduisons ci-dessous. Ce passage, qui commence par un positionnement par rapport à Newton et à Descartes, qui continue par quelques lignes un peu allusives sur Jean Bernoulli, a pour coeur la discussion sur la pertinence ou non d'utiliser le calcul des probabilités dans une question de ce type. D'Alembert en doute fort, contre Daniel Bernoulli...